This post is part of the F# Advent Calendar in English 2017 series organized by Sergey Tihon.
A while back I used the Meetup API to build a timeline of F# Meetup events across the globe
The timeline (circa May 2016): http://trelford.com/timeline/
You can find the source code in this Gist: https://gist.github.com/ptrelford/75fdf3f4c5dc9254736d88d35551c116
For this post I thought it would be fun to use the same Meetup API to focus in on the activity of the F#unctional Londoners Meetup group with an F# script.
The Meetup API returns a JSON response, making it an ideal place to use the FSharp.Data JSON Type Provider:
#r "../packages/FSharp.Data.2.4.3/lib/net45/FSharp.Data.dll"
let [<Literal>] auth= "&sig_id=10286388&status=past%2Cupcoming&sig=19c35f766e5b7a8cc163d2711749d8510a91de33"
let [<Literal>] url="https://api.meetup.com/fsharplondon/events?desc=true&photo-host=public&page=200"+auth
type Events = FSharp.Data.JsonProvider< url >
let events = Events.GetSamples()
This gives us types (and intellisense) over the JSON data, so I can make simple queries like the number of events per year:
let eventsbyYear =
events
|> Seq.countBy (fun e-> e.LocalDate.Year.ToString())
|> Seq.sortBy fst
Which returns:
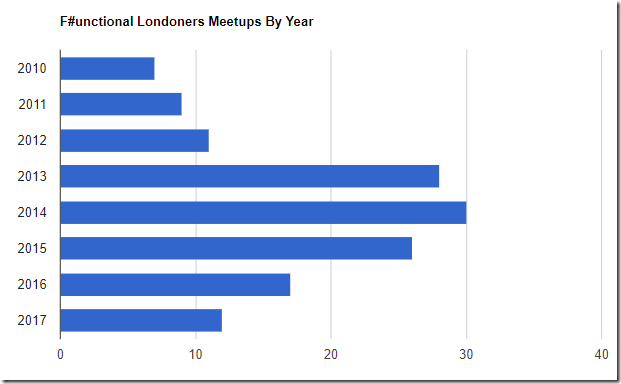
| Year | Meetups |
| 2010 | 7 |
| 2011 | 9 |
| 2012 | 11 |
| 2013 | 28 |
| 2014 | 30 |
| 2015 | 26 |
| 2016 | 17 |
| 2017 | 12 |
Next it would be interesting to get a plot, which can be easily achieved using XPlot:
#r "../packages/Google.DataTable.Net.Wrapper.3.1.2.0/lib/Google.DataTable.Net.Wrapper.dll"
#r "../packages/XPlot.GoogleCharts.1.4.2/lib/net45/XPlot.GoogleCharts.dll"
open XPlot.GoogleCharts
let years = eventsbyYear |> Chart.Bar |> Chart.WithTitle "F#unctional Londoners Meetups"
years.Show()
Here’s the nice bar chart result:
And for more detail down to the day we can use a Google Calendar chart:
let options = Options(title = "F#unctional Londoners Meetups", height = 1200)
let activity=
[for e in events -> e.LocalDate, 1] |> Chart.Calendar |> Chart.WithOptions options
activity.Show()
The white squares indicate a meetup event:
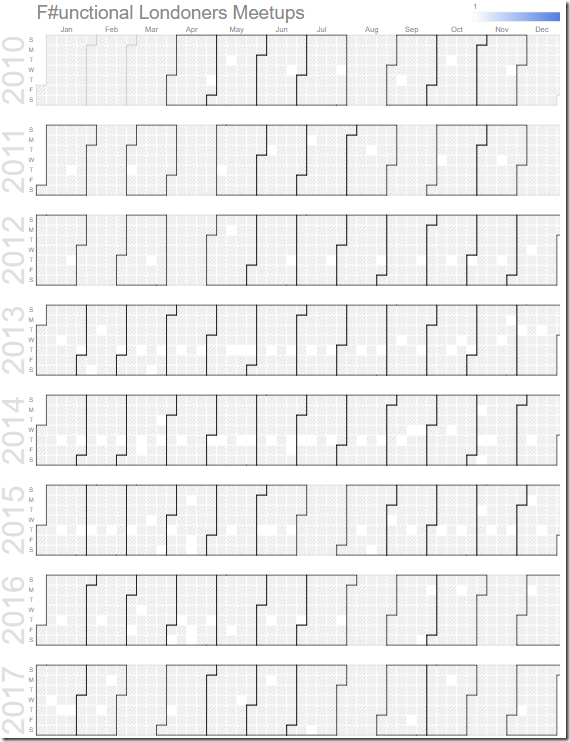
Looking at the data, we can see there’s been a meetup almost every month since the group started back in 2010, and back in April 2016 we managed 5 events in just one month!
We can also see that there’s been slightly less meetups over the last year and a half. This roughly coincides with the fact that I stopped working in London in early 2016. To this end, if somebody who is interested in F# AND lives or works in London would like to get involved in organizing the group, then please do get in touch.
That said the show will still go on (just a little less frequently), and we have a meetup scheduled this week on Thursday 7th December with Jorge Gueorguiev Garcia on Functional Calisthenics, so please do register and come along.