This month F# became the first functional programming language to hit the top 20 of the TIOBE Programming Community Index:
The recent rise in popularity of F# comes as no surprise. Apart from being a nicely designed language, F# is available in the latest version of Microsoft's Visual Studio (2010).
Functional programming is by no means a new concept in fact it has its roots in the Lambda Calculus developed in the 1930s. The first popular functional flavoured language Lisp was developed in the 1950s and ML, a language that F# owes much of its syntax to, was developed in the 1970s.
Some claim that functional programming concepts appear unfamiliar, in fact they are all around us, in Javascript, C#’s LINQ and even spreadsheets.. If you’ve ever written formulas in a spreadsheet then you’re already familiar with some of the principles of functional programming. The key building blocks of a spreadsheet are cells containing functions and values.
Over on Developer Fusion there’s a tutorial that demonstrates some key functional concepts while actually building a spreadsheet application in a couple of hundred lines of F#:
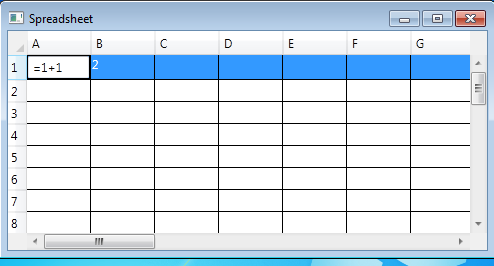
If you already have some F# or functional programming then why not give it a try, otherwise you might want to read on.
Functional Programming Basics
The following concepts are considered specific to Functional Programming:
- Pure functions
- First class and higher order functions
- Pattern matching
Pure Functions
Pure functions are functions that are free from side effects. That is pure functions always return the same result when called with the same parameters. Formulas in a spreadsheet hold this property.
First class and higher order functions
Functions are said to be first-class when they can be treated as first class objects. So like objects, functions can be passed as arguments to other functions, returned as values, assigned to values or stored in data structures.
Higher order functions are functions that take functions as their arguments. For example the LINQ Select method is an extension method that takes the function selector as a parameter:
public static IEnumerable<TSource>
Select<TSource, TResult>(
this IEnumerable<TSource> source, Func<TSource, TResult> selector)
Higher order functions are often used with anonymous functions as arguments. In the following line of code an anonymous function is passed to the Select function:
var squares = (new[] { 1, 2, 3 }).Select(n => n * n);
Support for higher-order and anonymous functions has been available in C# since 3.0 and will be available in C++ in the C++0x standard. They are also an integral part of JavaScript.
Pattern Matching
Many C based languages including C# supports basic pattern matching in the form of switch statements, matching against integral value and string types. In F#, and other ML based languages, a match statement is used instead:
| C# | F# |
| switch (day) { case 0: return "Sunday"; case 1: return "Monday"; case 2: return "Tuesday"; case 3: return "Wednesday"; case 4: return "Thursday"; case 5: return "Friday"; case 6: return "Saturday"; default: throw new ArgumentException("day"); } | match day with | 0 -> "Sunday" | 1 -> "Monday" | 2 -> "Tuesday" | 3 -> "Wednesday" | 4 -> "Thursday" | 5 -> "Friday" | 6 -> "Saturday" | _ –> invalidArg "day" "Invalid day" |
Functional programming languages allow pattern matching on types too. The following C# and F# code snippets are equivalent:
| C# | F# |
| abstract class Shape { } class Line : Shape { public Point Pt1; public Point Pt2; } class Square : Shape { public Point Pt; public float Size; } void Draw(Graphics g,Pen pen,Shape shape) { if (shape is Line) { var line = (Line)shape; g.DrawLin(pen,line.Pt1,line.Pt2); } else if (shape is Square) { var sq = (Square)shape; g.DrawRectangle(pen, sq.Pt.X, sq.Pt.Y, sq.Size, sq.Size); } } | type Shape = | Line of Point * Point | Square of Point * float let draw (g:Graphics,pen:Pen,shape)= match shape with | Line(pt1,pt2) -> g.DrawLine(pen,pt1,pt2) | Square(pt,size) -> g.DrawRectangle(pen, pt.X,pt.Y,size,size) |
In the code above the shape type is defined using an F# discriminated union, also known as algebraic data types in other functional languages like Haskell and Miranda. You can think of the type Shape as defining an empty abstract base class, and Line and Square as classes that inherit from the base class, just like the C# code to the left.
Note: The ‘*’ character in “Line of Point * Point” means “and”, i.e. a Line of Point and Point.
See Tomas Petricek and I implement the code above in the following video:
Starting F#
If you have Visual Studio 2010 then you already have F# installed, just start a New Project:
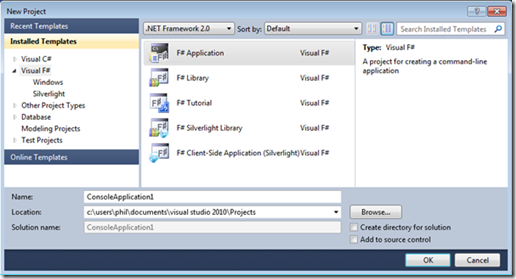
If you’re on Windows and don’t already have Visual Studio, you can also download the Visual Studio 2010 Shell for free and then install F#.
If you’re on Linux or Mac then you can use F# with Mono with MonoDevelop or Emacs. Or you can even edit F# code in your browser at http://tryfsharp.org.
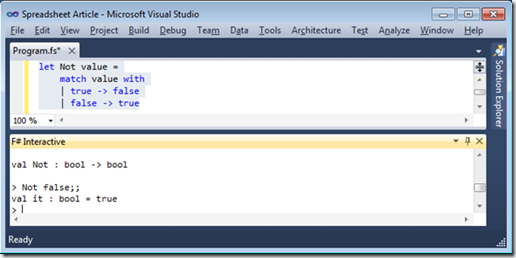
F# Interactive
You can try out your F# code immediately in Visual Studio using the F# interactive window. Just highlight the code and presss ALT+ENTER
F# Basics
F# is a statically typed functional programming language on .Net that aims to minimize the ceremony of coding. F# functions are first class so they don’t need to be defined inside a class and type inference means that most of the time the compiler will infer the types of objects for you.
Values
The let keyword is used to define values with type inference (like the var keyword in C#).
Values in F# are by default immutable (constant):
let alwaysTrue = true
Values must be marked explicitly as mutable if you want to be able to change them:
let mutable variable = 1
Functions
The following function uses a conditional expression, with its type is inferred as a function that takes a bool and returns a bool:
let Not value = if true then false else true
Pattern Matching
The Not function can also be written as a match expression:
let Not value =
match value with
| true -> false
| false –> true
This is the shorthand equivalent using the function keyword:
let Not = function true -> false | false -> true
Pattern matching can be also be used to match against tabular values:
let And p q =
match p, q with
| true, true -> true
| true, false -> false
| false, true -> false
| false, false -> false
One of the nice things about F# pattern matching is the added type safety. If a case is missing then the compiler gives a warning.
Discriminated Unions
A discriminated union is a type whose values can be any one of a set of types. You can think of it being like an enum in C# where each item has a specified type.
Option Types
The Option type is a simple example of a discriminated union, and it’s one that’s built into F#:
type Option<'TValue> = Some of 'TValue | None
The Option type is used when an actual value might not exist in which case it is specified as None, otherwise it is Some value. In F# the Option type is preferred over the use of null, and this helps remove a whole class of bugs.
Simple Parsing
Parsing a Spreadsheet formula based on whether it starts with an equals (‘=’) sign:
let parseFormula (s:string) =
if s.StartsWith "=" then Some(s.Substring(1))
else None
Parsing a decimal string value:
let parseNumber s =
match Decimal.TryParse(s) with
| true, n -> Some n
| false, _ –> None
For a primitive spreadsheet we could define cell values as being either formulas or numbers:
type value = Formula of string | Number of decimal
Now we can match a text string with the parsers for formulas and numbers:
let parse s =
match parseFormula s, parseNumber s with
| Some formula, None -> Formula formula
| None, Some number -> Number number
| _, _ -> invalidOp "Unknown value type"
Active Patterns
Active Patterns are defined inside banana brackets, i.e. ‘(|’, ‘|)’. An Active Pattern is a function that can be used actively inside a pattern matching expression.
The following Active Pattern returns whether a number is Odd or Even:
let (|Odd|Even|) n =
if i % 2 = 1 then Odd else Even
The Active Pattern can then be used in a match expression:
match 1 with
| Odd -> "Odd"
| Even -> "Even"
A partial Active Pattern goes one step further and tries to match a specified value returning an Option of either Some value if successful, or None otherwise.
The following FormulaText partial Active Pattern can use the same body as the parseFormula function we defined earlier:
let (|FormulaText|_|) (s:string) =
if s.StartsWith "=" then Some(s.Substring(1))
else None
As the following NumericValue can use the same body as the earlier parseNumber function:
let (|NumberValue|_|) (s:string) =
match Decimal.TryParse(s) with
| true, n -> Some(n)
| false, _ –> None
Now the Active Patterns may be used to simplify the earlier parse function:
let parse s =
match s with
| FormulaText text -> Formula text
| NumberValue n -> Number n
| _ -> invalidOp "Unknown value type"
What Next?
Time to put your new F# and functional programming skills to work and try creating your own Spreadsheet via the tutorial on Developer Fusion: